提要:针对实际工程,采用有限元法对钢筋混凝土转角楼梯的受力性能进行了分析,并与简化的计算方法进行了对比。分析结果表明,通过合理选择的有限元分析模型,较好地反应了转角楼梯的受力情况。根据有限元分析的结果选定简化的实用计算模型,通过计算,实用计算模型得到的结果与有限元结果相近,从而解决了以往转角楼梯这个空间超静定结构不能手算的课题。为了验证结论的正确性,在工程设计时,用实用计算模型得到的内力进行承载力计算,并将承载力计算的结果应用于实际工程。事实证明,本文建议的实用计算方法可靠,能够用到工程实践中,从而为以后钢筋混凝土转角楼梯的工程计算提供了理论计算依据。
关键词:钢筋混凝土转角楼梯,内力分析,计算方法
1 前 言
对钢筋混凝土转角楼梯,为避免其计算上的困难,传统的设计方法是在转角处通过设置钢柱或钢筋混凝土柱,这样的设计虽然从力学上讲传力比较明确,但不够美观,而且不够经济。虽然螺旋楼梯考虑了空间力学性能,不论从经济上还是从美观上都能得到良好的效果,但当场地受到限制时,螺旋楼梯同样不能满足业主的要求。本文分别采用比较符合实际模型的有限元法和简化模型的实用计算方法,对钢筋混凝土转角楼梯进行了受力分析,并将其结果应用于工程实际,从而克服了转角楼梯受力复杂难以手算的难题。
2 有限元法(FEM)
2.1 工程实例描述
某框支剪力墙结构,地下两层,1~5 层为商场, 6~30 层为住宅,总高度为100. 10m(阁楼除外) ,5 层高位转换,转换层高度为2. 22m。为了给住户提供一个美好的生活空间,根据业主的要求,需要设6 层到5 层屋面花园的楼梯,根据场地情况,只能采用转角楼梯,如图1 所示。
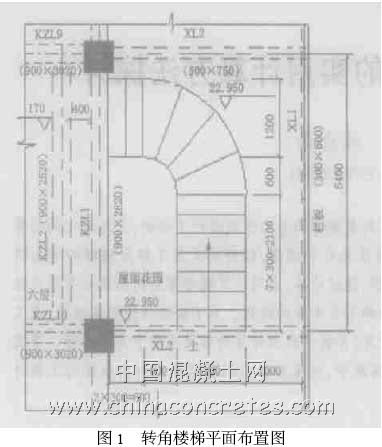
2.2 有限元分析模型(图2)
计算假定:
(1) 根据以往对钢筋混凝土楼梯的承载力计算,踏步板荷载均匀分布在整个梯段内。
(2) 根据转角楼梯的构造特性(A 支座的支座负筋锚入梁内,承担着负弯矩;A 支座和B 支座的下部筋锚入梁内,仅起构造作用) ,梯段按一端固定一端简支考虑。
根据业主及设计规范要求,取梯段宽度为1200mm ,厚度由计算确定。为施工方便,混凝土强度等级与转换层相同,即C45 ,泊松比取0. 2 ,仅进行静力计算。采用ANSYS 软件进行有限元分析,单元类型为SHELL93 。
荷载工况:为得到比较满意的挠度变形及为简化的实用计算方法提供可靠的理论依据,采用改变梯板厚度的方法实现加载,梯板厚度h 由80~180mm 变化,步长为10mm。参照螺旋楼梯的设计,考虑极限情况,梯板厚度由200~250mm 变化,步长为50mm。

荷载计算[1 ] :活载标准值取2. 0kN/ m2 ,分项系数取1. 4 ;恒载标准值(包括踏步板自重、装饰层等) 共计2. 747kN/ m2 ,分项系数取1. 2 ;荷载组合值为6. 096kN/ m2 。梯板荷载考虑分项系数1.2 后按自重考虑,重力密度为30kN/ m3 。
2.3 有限元法计算结果[2 ]
根据A NS YS 的计算结果,变形和内力列于表1 。
2.4 有限元结果分析
从表1 可以看出,当梯板厚度逐渐增大时,挠度的最大值逐渐减小; Y 方向的支座反力和绕Z轴的支座弯矩也随着变大; X 方向支座反力的绝对值在0. 81E - 5~0. 17E - 3 范围内变化,其值近似为0 , Z 方向的支座反力在0. 1E - 3~0. 154E - 3 范围内变化,其值也近似为0 ;绕Y 轴的弯矩为0 ;绕X 轴的弯矩(即扭矩) 随板厚的增大而增大,但其值很小。
3 实用计算方法(PCM) [ 3 ,4 ]
3.1 计算模型
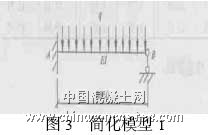
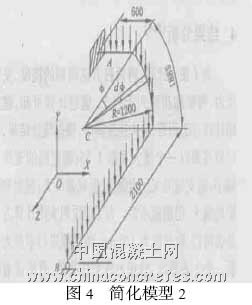
根据对有限元结果的分析,该结构的A 支座可看作Y 方向的线位移、绕X 轴和绕Z 轴的角位移为零,但其反力不为零,其它方向的位移和反力均等于零;B 支座在Y 方向的线位移为零,但其反力不为零。其他方向的位移和反力均等于零。通过该结构的静力分析和几何构造分析,该结构是空间的一次超静定结构,因此,只要得到一个未知量,其他未知量也就迎刃而解了。因此,为便于比较和手算,可取均布荷载作用下一端固定一端简支的单跨梁(图3) 来计算跨间的最大挠度和支座B 的反力,然后按图4 来计算其他内力。
3.2 计算公式及结果
有限元分析中,将梯板自重按体力狡算,因此,在实用计算中应将其按均布的恒载考虑。内力及变形的公式推导如下:

式中,L 为转角楼梯的中线长度。
由式(1) ~式(6) ,可知不同梯板厚度的内力和变形(见表2) 。
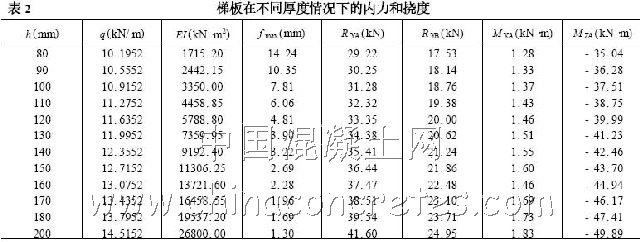
4 结果分析[ 5 ,6 ]
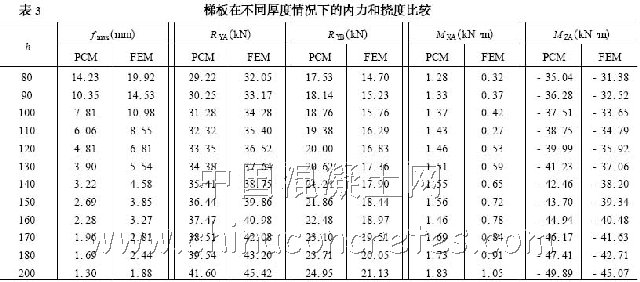
为了便于比较,将两种方法得到的挠度、支座反力、弯矩和扭矩列于表3。通过比较可知,就实用计算方法而言,最大挠度偏小,根据统计结果,可以对其乘以一个增大系数1. 35 ;固定端的支反力偏小,简支端的支反力偏大,但误差不大;扭矩和弯矩均偏大,但偏值不多。为了能说明实用计算方法是否可行,取厚度为120 mm 的梯板进行承载力分析。由上表看出,梯板为弯剪扭构件,弯矩比有限元法略大,因此仅考虑剪扭情况。为安全起见,设环境类别为二类b ,即保护层厚度为20 mm。由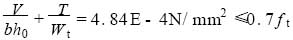

可知,不必通过计算配筋,仅按构造配筋即可。为进一步说明问题,仍取梯板厚度为120mm ,但其内力按200mm 的梯板考虑,即相当于活载约3. 7kN/ m2 (规范最大值为3. 5kN/ m2) 。由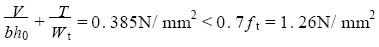
可知,同样不必通过计算配筋,仅按构造配筋即可。
5 结 论
通过以上分析,可以得到如下几点结论:
(1) 实用计算方法得到的结果与有限元解基本相近,因此可以应用于工程实际中。本结论已在工程中得到验证。
(2) 实用计算方法得到的挠度应乘以1. 35的放大系数。
(3) 按照一端固定一端简支的平面梁求简支端的支座反力,其余内力按照实际的空间杆系结构模型(其中,一端仅考虑一个支座反力,且该支座反力等于平面梁简支端的支座反力) 进行计算。
(4) 按照实际计算得到的弯矩进行正截面承载力计算;一般情况下可忽略剪力和扭矩,对其按构造配筋。
参考文献
[1 ] 建筑结构荷载设计规范( GB50009 - 2001) . 北京:中国建筑工业出版社, 2001
[ 2 ] 刘 涛,杨凤鹏主编. 精通ANSYS. 北京:清华大学出版社, 2002
[3 ] 《建筑结构静力计算手册》编写组. 建筑结构静力计算手册. 北京:中国建筑工业出版社. 1988
[4 ] 龙驭球, 包世华等. 结构力学教程. 北京:高等教育出版社,2002
[5 ] 程文襄, 康谷贻, 颜德 . 混凝土结构. 北京:中国建筑工业出版社,2002
[6 ] 混凝土结构设计规范( GB50010 - 2002) . 北京:中国建筑工业出版社, 2002

















