摘 要：基于退化壳原理，考虑火灾下板壳截面的不均匀温度场分布而引入分层模型，同时在每分层上考虑材料在不同温度下的热力弹塑性本构关系，建立了火灾下钢筋混凝土板壳结构的有限元数值计算模型。另外，通过全拉格朗日方法考虑了大位移的几何非线性影响。最后通过一钢筋混凝土板在高温下的试验进行了验证，并分析了配筋率和保护层厚度的影响。结果表明：提出的火灾下钢筋混凝土壳单元数值计算模型的计算结果与试验结果吻合较好，可以用来分析火灾下钢筋混凝土框架结构楼板的反应。
关键词：钢筋混凝土板壳；火灾反应；分层模型；薄膜作用；非线性分析
1引言
混凝土板壳结构是实际工程中常见的结构形式。由于钢筋混凝土楼板在实际火灾中对防止结构破坏起着重要的作用，研究者们[1,5]对混凝土板壳进行了抗火试验与理论研究，由于火灾试验费用高，周期长等原因，近年来，数值模拟分析作为一种经济有效的研究方法受到广泛重视。早期的研究者在研究框架结构耐火性能时不考虑楼板的作用，或把楼板等效为梁单元进行分析[4]，与实际情况有一定出入。随后，Linus Lim[6]建立了四结点四边形板单元，对混凝土楼板高温反应进行了分析，这比等效梁方法取得了更加准确的结果。一些真实的火灾事例和试验表明，结构中的楼板在火灾中有时会出现薄膜作用，对结构的受力形式产生影响。Mohamad[5]等认为采用壳单元可以准确、有效地模拟钢筋混凝土楼板的火灾反应，尤其是模拟楼板在火灾中表现出的弯曲和薄膜作用。Huang[12]在分析混凝土楼板火灾反应时，就建立了平板壳单元模型，并开发了相应的计算程序VULCAN。
本文在这些学者的研究基础上，基于退化壳理论，建立了考虑不同温度影响的通用壳单元模型。为了考虑火灾下板壳截面的不均匀温度场分布，引入了分层模型，同时在每分层上考虑材料在不同温度下的弹塑性本构关系，从而准确地模拟混凝土材料的开裂、屈服与压碎现象。另外根据全拉格朗日方法，推导了壳单元切线刚度矩阵，来反映楼板结构发生大位移后的薄膜张拉效应。最后用一钢筋混凝土板抗火试验验证了本文模型的准确性和有效性。
2 分层壳单元计算模型
本文的壳单元是基于退化壳理论建立的八结点四边形单元如图1所示，通过引入Hinton[13]分层模型把壳单元划分成可以考虑不同材料性能的相应层，钢筋可以用等效厚度的均匀钢层模拟，只具有轴向强度和刚度，通过其与整体坐标系下的夹角来考虑刚度对其他方向上的影响。假设混凝土层和钢层无相对滑移，每层温度分布均匀，采用9点高斯积分，在每层每个高斯点处可以分析混凝土开裂、压碎和钢筋屈服情况。
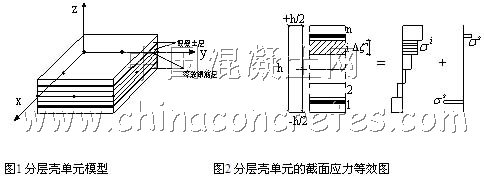
许多学者对高温下材料在的物理和力学性能进行了研究，提出了许多重要的计算公式。利用这些公式和高温下的材料本构关系可以进行结构火灾分析[6]。本文采用高温下材料的热力弹塑性本构关系来分析钢筋混凝土板在火灾下的反应，在高温下材料总的应变增量可表示为[9]： 
= 
+ 
+ 
+ 
+ 
(1)
式中 
为弹性应变； 
为材料属性变化引起的变形；
为热应变增量； 
为徐变增量； 
为塑性应变增量。
考虑等强硬化模型： 
，最终的增量本构方程为[9]：
= 
- 
( 
+ 
+
)- 
(2)
式中 
为热力弹塑性本构矩阵， 
为高温影响的材料膨胀系数，
= 
， 
= 
，
= 
- 
且 
= 
T 
/ 
3)
本文壳单元模型中，在每一分层的每一个高斯点处假设：
= 
( 
- 
- 
)= 
(4)
为增量步中总的热应变增量，根据上面的增量本构方程(2)可知：
= 
+ 
+ 
(5)
壳单元应变能增量为：
=1/2 
= 
(6)
壳单元表面分布力做功为：
=- 
(7)
则系统总位能为： 
= 
+ 
(8)
= 
- 
- 
- 
=0
由系统最小位能原理：
故单元求解方程为：
= 
+ 
+ 
= 
(9)
通过刚度集成即可求解系统位移增量。
当考虑大位移的影响时，每一分层上的单元应变位移矩阵 
可分解为线性部分 
和非线性部分 
，
= 
+ 
则 
= 
10)
由单元内外力平衡条件：
= 
- 
= 
- 
=0 (11)
对(11)由变分原理可得单元切线刚度矩阵 
：
= 
+ 
- 
=0 (12)
令 
= 
由 
= 
则
= 
+ 
= 
+ 
= 
+ 
(13)
= 
+ 
(14)
式中， 
为式(9) 中的单元刚度， 
= 
为即时应力附加几何矩阵。
为了得到 
，还需要求出 
，考虑VonKarman假设： 
， 
对 
， 
， 
的导数为微小量， 
对 
的变分可以忽略，利用全拉格朗日方法[13]：
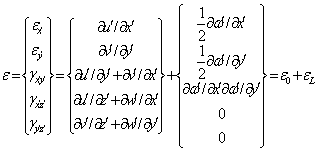(15)
非线性部分可表示为：
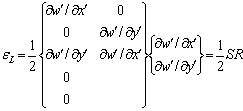(16)
R可以用位移矢量 
以及单元形状函数表示为：
R= 
=G 
(17)
式中G由单元形状函数确定的矩阵。
则 
=1/2SG 
。 (18)
对(16)进行变分： 
=1/2 
+1/2 
=S 
=SG 
则 
= SG，在程序中首先计算出 
和G，再用当前位移求出S，从而可以求出 
，再迭加到 
中得到最终的应变位移矩阵 
。通过对(13)进行高斯积分可求得 
，并根据当前应力求出几何矩阵 
，最后根据(14)求出 
。
3 高温材料模型
3.1混凝土
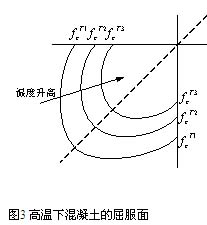
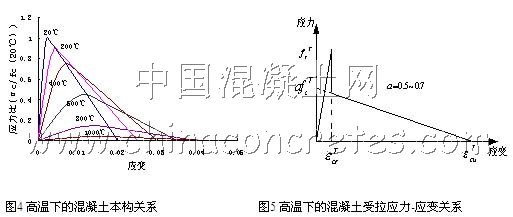
本文采用Drucker-Prager屈服准则和应变硬化模型来分析混凝土的受压状态，因为垂直于壳中面的应力忽略不计，其应力状态和双轴应力状态差别不大，但是混凝土材料在高温下的双轴本构关系研究很少，这里假设高温下的屈服面形状和常温下的一样，而相应的抗压强度则采用高温下的抗压强度值(见图3)。为了用一种适合于数值计算的形式来描述混凝土的本构关系，E. Hinton[13]根据双轴试验结果以及对等双轴屈服强度和单向屈服强度关系的假设，使Drucker-Prager屈服条件成为只含等效应力的函数：
(19)
式中 
为等效应力。这样根据应变硬化模型和高温下混凝土的单轴本构关系就可以进行高温下的屈服判断。具体的混凝土在高温下的单向受压应力-应变关系如图4所示：上升阶段采用EC4[10]中混凝土高温本构关系表达式，软化阶段采用了直线表示，而压碎条件的判断也采用与式(19)相似的表达式，假定等效应变达到极限应变 
后认为混凝土压碎并退出工作。
混凝土的受拉应力应变关系假设为直线，开裂区采用双裂缝模型，并采用最大拉应力控制准则假定当最大主应力达到了在高温下的抗拉强度 
，在垂直主应力方向产生裂缝。 
根据不同的温度确定[2]： 
/ 
=1-T/1000， 
取为0.1 
。为了模拟开裂后裂纹之间的拉伸刚化作用，采用了逐渐减小的垂直于开裂面的应力分量来表示(见图5)。开裂应变 
= 
/ 
，当超过极限开裂应变 
时，则认为没有粘结作用， 
取为10 
。另外，混凝土热膨胀系数 
取为[2]：28(T/1000)×10-6/℃。
混凝土的徐变模式采用文献[11]中的模型：
(19)
式中： 
且 
3.2钢筋
高温下钢筋采用理想弹塑性模型，其屈服强度 
和弹性模量 
分别为[11]：
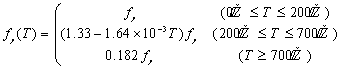(20)
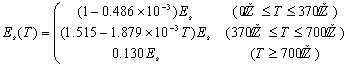(21)
式中 
， 
分别为常温下钢筋的屈服强度和弹性模量。
钢筋的徐变模式采用Norton徐变模型[9]：
(22)
式中 
=0.37×10-4exp(0.000337/T)
=8.1×10-4[1-4.7×10-4(T-300)]
另外钢筋热膨胀系数取为：0.5 
×10-6/℃。
4 非线性求解过程
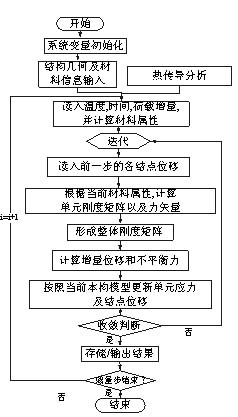
为了进行钢筋混凝土结构火灾反应分析，作者同时编写了结构火灾瞬态热传导分析程序(由于篇幅有限，在此不再赘述)，在这里直接用来进行楼板热传导分析，并假定混凝土裂缝对热传导没有影响。进行结构分析时，程序对整个时间域以及外荷载划分为一定数量的增量步，每一增量步内的非线性方程组的迭代求解采用了Newton-Raphson迭代方法，分析过程见图6。
在高温结构分析中，因为不平衡力常可形成平衡的力系，所以迭代过程中，使用力的收敛准则不很合适，其解不一定单调收敛，所以本文同时采用结点不平衡力准则和结点位移增量准则来控制收敛。
5 数值算例
为了验证本文提出的分层壳单元的数值模型，本文用西安建筑科技大学陈礼刚所做的钢筋混凝土板抗火试验[1]来进行验证。该试验中钢筋混凝土板试件尺寸为 4.3m×1.5m×0.12m，采取试验炉墙壁进行简支的方式，允许转动但限制竖向位移。板底部布置了两层钢筋，分别具有0.524mm和 0.113mm的等效厚度。
由于试验中采取了ISO834标准升温方式，在热分析时采取标准升温曲线来模拟火灾环境。热分析程序中将混凝土板沿厚度划分成6层，每层离散成四个三角形单元。根据试验情况板底热交换系数取40W/( )，混凝土表面与试验炉表面辐射率取0.7。本文热传导分析程序的分析结果见图7和图8。图7比较了各时刻板截面温度分布和试验结果；图8表明在试验过程中板截面中点的温度和实测温度符合良好。
在结构分析程序中混凝土板沿厚度划分成6层，钢筋等效成0.524mm 和 0.113mm的两层钢层，刚度方向分别为纵向和横向。由于荷载以及边界条件的对称性，对其四分之一进行结构分析。表面分布荷载为2KN/m2，本文计算的中点竖向位移与试验结果、文献[1]中ANSYS计算结果进行了比较(见图9)。由图9可见在温度小于500℃时，计算值与试验值相差不大，这是由于材料力学性能变化较小，热膨胀占主要影响，板基本处于弹性阶段。之后随着温度的升高，材料强度和刚度的明显降低，挠度快速增长，由图9可见按本文计算模型计算的结果比文献[1]的ANSYS计算结果更加合理。同时由比较可知，在较低温度时，材料膨胀特性是导致结构变形的主要应因素，随着温度的升高，材料强度和刚度的降低变为主导因素。另外，图10表示了在温度达到978℃时板底单元高斯点裂缝出现的情况。
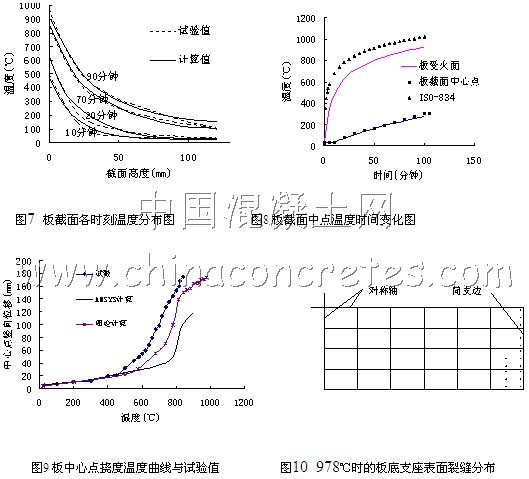
6 参数分析
钢筋混凝土板构件的耐火性能受许多因素的影响，本文主要考虑配筋率和保护层厚度。用上述钢筋混凝土板为分析对象而分别改变其配筋率和保护层厚度。图11比较了在相同恒定荷载作用下不同配筋率时板的挠度随温度的变化情况，在温度小于500℃时，配筋率的影响不大，当温度大于500℃后，低配筋率板的挠度变化明显快于高配筋率的混凝土板的挠度变化。可见适当提高配筋率可以改善板的耐火性能。
另外，因为混凝土是热惰性材料，混凝土板截面存在较大的温度梯度，并且由于在热分析时，不考虑保护层出现的裂缝对热传导的影响，所以随着保护层厚度的增加，受拉区钢筋位置的温度也就越低，从而钢筋混凝土板的刚度就越高，图12反映了不同保护层厚度时钢筋混凝土板的挠度随温度的变化情况，在温度较低时，混凝土保护层厚度对板的挠度影响较小，当温度迅速升高后，保护层厚度较大的板比保护层厚度小的板中点挠度增大程度有所减小，这与文献[1]得出的结论类似。
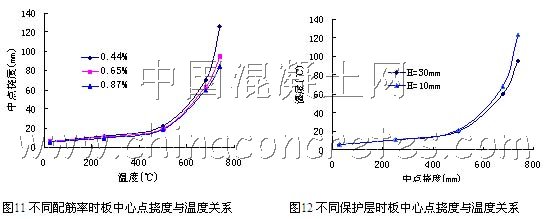
7 结语
结构在高温和和荷载共同作用下的性能反应十分复杂，实际工程中的每个结构不可能都靠模型试验来确定其高温承载力或耐火极限。本文主要进行了以下工作：
(1)根据退化壳理论，引入分层模型，建立了钢筋混凝土楼板结构的火灾反应有限元数值分析模型。
(2)与具体试验结果进行了验证比较。结果表明，本文的建立的模型以及分析程序可以用来分析结构中混凝土楼板的火灾反应。
参考文献:
[1] 陈礼刚. 钢筋混凝土板受火性能的试验研究.西安建筑科技大学博士学位论文.2004.
[2] 过镇海,时旭东.钢筋混凝土的高温性能及其计算 清华大学出版社.2003
[3] 江见鲸,陆新征,叶列平.混凝土有限元分析清华大学出版社.2005.
[4] 姚亚雄,朱伯龙.钢筋混凝土框架结构抗火性能试验研究.同济大学学报,1996,24(6): 619-624
[5] Mohamad J.Terro. Numerical modeling of the behavior of concrete structures
in fire. ACI Structural Journal/March-April, 183-193.1998.
[6] Linus Lim. Numerical modelling of two-way reinforced concrete slabs in fire
Engineering Structures 26 (2004) 1081-1091
[7] 王勖成,邵敏. 有限单元法基本原理和数值方法. 清华大学出版社.1997
[8] M.B.Wong. Plastic frame analysis under fire conditions. Journal of Structural
Engineering, March,290-296,2001.
[9] Tai-Ran Hsu. The finite element method in thermomechanics.
Allen&Unwin. 1986.
[10] Eurocode 4: Design of Composite Steel and Concrete Structures.
Part 1.2: Structural Fire Design, CEN/TC250/SC4 N39, Commission of the European
Communities, Brussels, 1993.
[11] 陆洲导,朱伯龙. 钢筋混凝土框架火灾反应分析.土木工程学报.1995.12.18-27
[12] Huang Z, Burgess IW, Plank RJ. Nonlinear analysis of reinforced concrete
slabs subjected to fire. ACI Structural Journal 96(1):127-35.1999.
[13] E. Hinton, and D.R.J. Owen. Finite element software for plates and
shells, Pineridge press,swansea. 1984
