摘要 用自行设计的混凝土渗透试验装置研究了混凝土渗透参数的演变规律。发现在压力水作用下,混凝土在短时间内渗透速率达到最大,随后就逐渐降低并趋向于稳定值。根据试验结果提出了混凝土渗透系数的时变模型。
关键词 混凝土 渗透 混凝土渗透试验装置 时变模型
中图分类号: T528 文献标识码: A
0 引 言
渗流溶蚀是水工混凝土构筑物破坏的主要形式之一。水工混凝土在水压力的作用下,会发生渗透和渗流,后者会引以混凝土中水泥石组成的溶蚀破坏,因此渗透性是水工混凝土构筑物中最为关注的特性之一。由于混凝土的水渗透性较低,通常用混凝土在特定试验条件下能承受的(水不渗透)最大或在一定水压下持续一段时间后的渗透高度来表征混凝土的抗水渗透性能[1],也有用气体渗透性表征渗透性的[2-3],而对混凝土渗透以后的渗透性研究较少。阮燕[4]等研究了在1.2~2.8 MPa水压下面板混凝土的渗透溶蚀过程,发现渗透系数随渗透历时的延长而降低,逐渐趋于某一特定值。但文献[4]未提供关于渗透系数经时变化规律的更多信息。
笔者曾用自行设计的混凝土渗透试验装置研究了持续压荷载作用下混凝土的渗透性与荷载的关系[5],本文仍采用该装置研究持续水压力下混凝土的渗透性的经时变化规律。
1 实 验
1.1原材料与试件
1用南京龙潭水泥厂生产的P·O 32.5级水泥,南京热电厂的Ⅱ级粉煤灰,细度模数为2.5的河砂,最大粒径10 mm的石灰岩碎石及自来水按表1所示配合比配制混凝土,成型成内、外直径分别为30 mm 和110 mm的圆筒形试件,每组试样成型六个,其中两个用于渗透试验,三个用于强度测定,另一个备用。试件在混凝土标准养护室养护28 d后,用切割机将试件两头截去,得到高度为110 mm的试件。取其中三个试件测定混凝土试件抗压强度,结果见表1。

1.2 实验方法
实验所用混凝土渗透试验装置见图1。该装置使用4根对称布置大吨位压缩弹簧作为加压部件。装置工作时由高立柱压力试验机对弹簧加压,压力值大小则由读取压力机表盘数值来控制,到达规定压力值时立即将螺栓拧紧并关闭压力机,此时试件所受的外部压荷载就由弹簧提供了。由于弹簧弹力受混凝土变形等因素的影响很小、保压性能良好并且应力损失小、不受外部断电等干扰因素的影响,故可以进行长时间的压应力状态下混凝土渗透溶蚀等性能的研究[5]。弹簧产生的压力通过钢板、球座、上压板传递作用到试件上。上压板内部钻一φ 5 mm的小孔,在钢垫板外设接口用铜管接至砂浆抗渗仪压力水出口,压力水由砂浆抗渗仪提供并流经铜管和上压板内部的小孔作用于圆筒形试件的内表面,水压由砂浆抗渗仪上的压力表调节控制。试件外表面浸在注满水有机玻璃套筒中,套筒上方用橡胶皮盖住以避免蒸发。套筒上有一控制水位的溢流孔,用一塑料管连接溢流孔和放于低处的量筒,这样透过环型试件壁的渗透水量可以通过量筒收集。
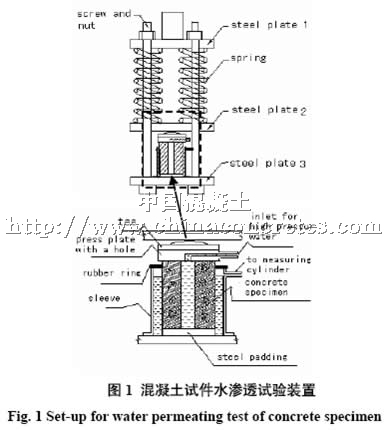
试验时试件先用环氧树脂砂浆粘贴在上下两块钢垫板上,待环氧树脂硬化后进行真空饱水, 以便在试验时尽快达到渗透稳定。在本研究中分别对试件施加5MPa的轴向压力,对C1和C2混凝土所施加的稳定水压分别为0.8 MPa和1.2MPa,即试件中水力梯度分别为20MPa和30MPa,水压过高(对C1和C2分别超过1.2MPa和2.0MPa)时,试件会很快被水击穿。
加用稳态法测量混凝土渗透系数时,由于其渗透性很小,要使足量的水透过混凝土以保证测量精度,因此每次累积4 h的渗透水量,用电子天平称取其质量,并计算4 h内的平均渗透系数。
根据单位时间的渗透水量计算混凝土试件的渗透系数。对圆环形试件渗透系数计算公式由达西公式推导得。达西公式为.[6]:

式中:
Q—单位时间内的流量(cm3/s);
K—渗透系数(cm/s);
A—过水面积(cm2);
ΔP—水流入面和流出面间的水头差(cm);
L—渗透距离(cm)。
上式未考虑温度对液体粘度的影响。
达西公式要求孔隙平行不发生横向渗透,对于混凝土这种内部孔结构复杂且不断变化的材料是做不到的,但目前国内外学者认为达西定律对于水泥混凝土还是适用的,对圆环形试件我们假设仅发生径向渗透,对式(1)作微分得式(2)

即:
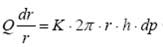
再对式(2)两边作积分,
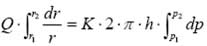
这样就得到圆环形试件渗透系数计算公式(3),
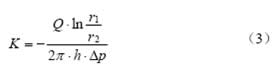
式中K—渗透系数(cm/s);
Q—单位时间内收集的水流量(cm3/s);
r2—环状试件的外半径(cm);
r1—环状试件的内半径(cm);
h—环状试件的高度(cm);
Δp—水流入面和流出面间的水头差(cm)。
2 结果与讨论
2.1 渗透现象与渗透系数变化
图2是两组混凝土试件(每组两个)渗透系数K随时间t的变化。从试件透水开始,可以观测到渗水量短时间内会有一段波动变化的过程,但其总趋势是显著增加。这是由于在混凝土试件在受水压作用后,开始只是局部透水,随着时间的延长,透水面上各部分均开始透水,或者较大的水力梯度形成了一些原本封闭的孔打开,造成孔结构的一些改变而造成的。水量很快到达最大值后即开始下降,图2的渗透时间均是从渗水量达最大值开始计时。
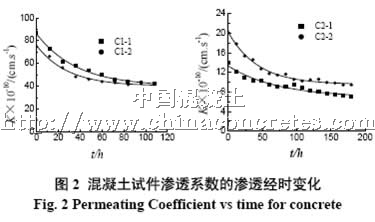
渗透系数在达到最大值后随时间下降可能有下列原因:①被压力水冲下的碎颗粒及杂质随水流在一些部位沉淀堵塞;②水泥熟料的持续水化和一些可溶性物质如氢氧化钙,发生碳化反应而生成碳酸钙或沿渗流通道结晶,使渗流量减小。
本试验的观测结果表明渗透系数下降最明显的是在渗透出水达到最大值后约40~60h以内,其后仍会随着渗透时间的增加比较平缓的下降。
试件C1和C2比较,C1不仅开始透水的时间比C3早,渗水后亦能较快达到最大流量。同时从图中也发现渗透相对平稳阶段所用时间也比C3试件少。这宏观上与强度、水灰比、水泥用量有关,微观上则与其中孔的尺寸、分布、连通以及集料与水泥石的界面微观结构密切相关。
从图2还可看出,无论是C1和C3,同一配合比的两个试件实验数据都呈现出一定的离散性。这也说明了就渗透性而言,混凝土是一种很不均匀的材料。本试验试件尺寸比较小、混凝土存在缺陷等偶然因素可能也是一个重要原因,而且由于实验周期比较长,发生意外的概率也比较高。
2.2渗透时变模型与稳定性的分析
对于各组混凝土试件,可以看出的渗透系数随着渗透时间增加而减小这一现象有一定规律性,且各条曲线形式大体相同,试验数据虽有一定离散性但在一个数量级,对各组试件的的渗透系数与时间关系按式(4)拟合,

式中:t—时间(h);
k—渗透系数(10-10cm/s);
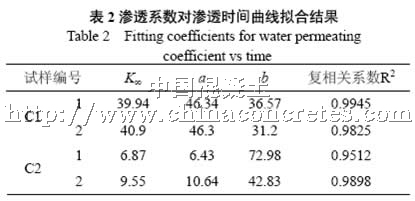
k∞、、b—拟合参数,见表2。 a
从表2中可以看出,由式(4)拟合曲线与实验结果拟合较好,相关系数R2大于0.95。因此式(4)较好地反映了水工混凝土渗透系数的时变过程:渗透系数随渗透时间呈负指数函数减小,开始时渗透系数迅速减小,随着渗透时间的增加则渗透系数下降越来越平缓,当渗透时间足够长时,式(4)右边第2项趋向于0,因此k∞即为预期的稳定渗透系数。
这里要特别指出的是,本试验是在渗水量最大值后才能开始计算渗流的渗流量的经时过程,由此推得渗透系数随渗透时间增加而减小的规律。而在实际工程中,当坝体混凝土出现隐患病害、或高应力比(≥60%)以及高水力梯度,使裂缝的自愈现象逐渐消失(即裂隙中CaCO3的被渗流水析出)等情况时,渗透系数会显著增大.
3 结 论
(1) 当水力梯度低于某个临界值时,混凝土在短时间内渗透速率达到最大,随后就逐渐降低并趋向于稳定值。
(2.) 混凝土的渗透系数随渗透时间的减小近似呈负指数函数规律。
参考文献
1 中华人民共和国国家经济贸易委员会. 中华中华人民共和. 2001-12-26
2 PICANDET V, KHELIDJ A, BASTIAN G. Effect of axial compressive damage on gas permeability of ordinary and high-performance concrete [J]. Cem Concr Res, 2001,31(11):1 525
3 TAKAFUMI S, THEODORE W B, THOMAS A H. Effect of stress on gas permeability in concrete [J]. ACI Mater J, 1996, 93(5):443
4 阮燕,方坤河,吴玲. 混凝土的渗透溶蚀特性研究 [J]. 水力发电学报,2001,(1):31
5 方永浩,李志清,张亦涛. 持续压荷载作用下混凝土的渗透性[J].硅酸盐学报,2005, 33(10):1281
6 顾慰慈 著.渗流计算原理及应用.北京:中国建材工业出版社,2000

















