摘要:收集了158 根集中荷载作用下高强混凝土无腹筋梁的抗剪试验数据,将抗剪强度试验结果与中国规范(GB50010-2002)和ACI 规范(ACI318-2002)理论计算结果相比较,并分析了混凝土强度、剪跨比、截面尺寸和纵筋配筋率对梁抗剪强度的影响。结果表明:中国规范公式对小剪跨比梁偏于保守,对大剪跨比梁不够安全;ACI 公式高估了混凝土强度的影响,低估了剪跨比的影响,计算结果偏于保守;两公式均没有合理考虑甚至忽视了尺寸效应和纵筋配筋率对梁抗剪强度的影响。
关键词:高强混凝土;无腹筋梁;抗剪强度
1 引言
梁斜截面抗剪承载力问题是混凝土结构基本理论中的经典问题之一。因其破坏机理复杂,影响因素众多一直备受国内外学者关注。近一百年来,国内外对混凝土梁在不同荷载作用情况下的抗剪性能进行了大量的试验研究,采用了非常精巧的分析工具,但是仍然没有完全弄清楚。各国规范提供的抗剪承载力计算公式,大多是通过对大量的实验结果的分析,同时采用数理统计方法建立起来的。
美国混凝土协会提出圆柱体抗压强度设计值大于41Mpa 的混凝土为高强混凝土,我国根据当前的设计和施工水平,认为混凝土强度等级大于C50 的混凝土为高强混凝土[1]。随着经济水平的不断提高,高强混凝土在工程中的应用越来越普遍。由于高强混凝土水泥用量大,流动性较大,与普通混凝土相比,脆性增加,性能上也有所不同。现行规范公式用于高强混凝土无腹筋梁抗剪强度计算,对抗剪强度各主要影响因素的评估是否仍然合适,会否造成计算的安全度降低,是有待研究解决的问题。
2 高强混凝土无腹筋梁抗剪试验概况
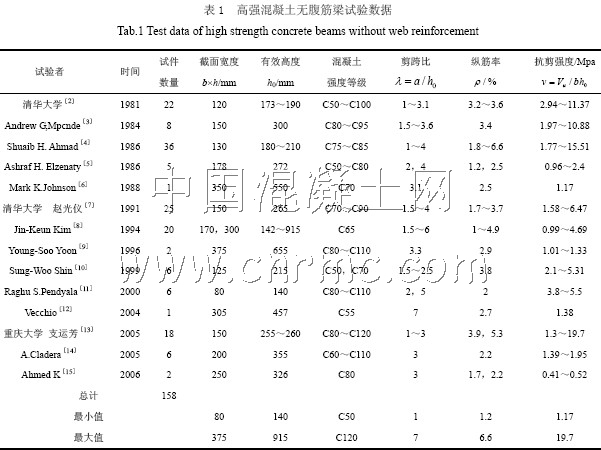
本文收集了从上个世纪八十年代以来,国内外研究者进行的高强混凝土无腹筋梁在集中荷载作用下抗剪承载力试验的数据共158 个,列于表1 中。从表中可见,国外研究者的试验数据较多,国内只收集到清华大学[2][7]和重庆大学[12]的试验数据。所列数据的高强混凝土梁均为矩形截面,试验变化的参数主要为梁的混凝土强度等级,剪跨比和纵筋配筋率。所有试验数据中混凝土强度等级均在C50 至C120 之间,剪跨比在1~7 之间,纵筋配筋率在1.2~6.6 之间。Kim[8]的试验除了考虑以上三种因素以外,还探讨了截面有效高度对梁抗剪强度的影响。
3 试验值与计算值的比较分析
对收集到的试验数据,分别根据我国规范GB50010-2002 抗剪公式(1)和ACI 318-2002抗剪公式(2)进行抗剪强度的计算。将试验值与计算结果的比较列于表2,可见vtest/vChina的均值为1.4,离散系数为0.512;而vtest/vACI的均值为2.68,离散系数为0.715。表明对于高强混凝土无腹筋梁的抗剪强度计算,ACI 规范安全度较高,但是偏于保守,中国规范的试验结果符合情况相对较好,但是安全度有所降低。
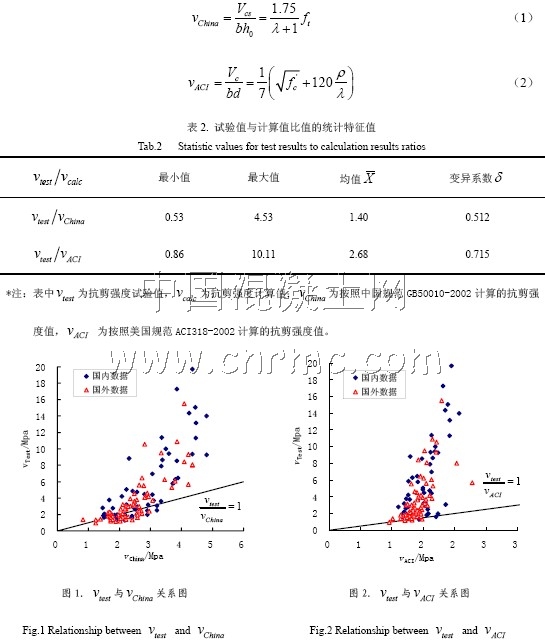
图1给出中国规范公式计算值与抗剪强度试验值的散点图,图中显示对试验抗剪强度vtest≤3.5Mpa 的梁,有相当一部分点落在了vtest/vChina=1以下;而当vtest >6Mpa 时,试验值又远远大于计算值。进一步研究发现抗剪强度vtest/vChina<1的数据共有41 组,除少数为剪跨比为2 以外,均为剪跨比λ > 3的梁;而vtest>6Mpa 的试验数据共有27 组,除4 组为剪跨比λ = 2 的梁,其余均为λ =1~1.5的梁。由此可见,中国规范公式用于高强混凝土无腹筋梁时,对于小剪跨比的梁偏于保守,对于大剪跨比的梁则不够安全。图2 给出ACI 公式计算值与试验值的散点图,图中除了5 个点试验值小于计算值以外,其余的试验值均大于计算值,部分数据远远高于计算结果。进一步研究表明vtest/vACI<1的5 根梁均为剪跨比λ > 3的梁,试验值远远高于计算值的梁多为剪跨比较小的梁。可见, ACI 规范公式计算结果偏于保守,但是对剪跨比大于3 的梁不够安全。
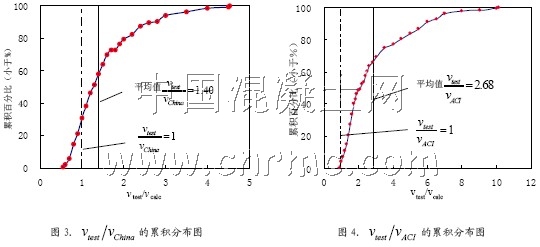
为了更直观的体现试验抗剪强度小于计算抗剪强度的梁所占的比例,做试验值与计算结果比值的累积布图于图3和图4。图3显示,试验值与中国规范计算结果比值vtest/vChina小于其平均值1.40 的数据占总数据的58%,vtest/vChina<1的数据占总数据的31%。图4 表明,试验值与ACI 规范计算结果比值vtest/vACI小于其均值2.68 的数据占总数据的68%,vtest/vACI<1的数据占总数据的4%。
4 无腹筋梁抗剪承载力影响因素
影响梁抗剪承载力的主要因素为混凝土强度、剪跨比、截面有效高度和纵筋配筋率。下面将所收集到的国内外研究者的试验数据分别按以上几种因素进行分析。
4.1 混凝土强度等级
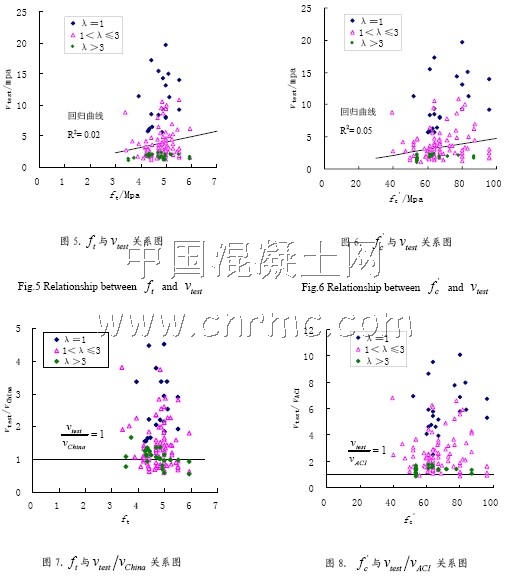
无腹筋混凝土梁的剪切破坏最终由混凝土材料的破坏控制,所以其剪切承载力随混凝土的强度而提高。不同剪跨比的梁,因其破坏形态的差别,承载力分别取决于混凝土的抗压和抗拉强度。中国规范用的是混凝土抗拉强度ft,美国规范用的是混凝土圆柱体抗压强度fc。在图5和图6中分别给出混凝土抗拉强度ft和抗压强度fc与梁抗剪强度试验值vtest 的关系图,图中可见,vtest与ft和fc有大致的线性关系,但是数据的离散性很大,回归曲线的相关系数都很低。图7 给出了抗剪强度试验值与中国规范计算值比值vtest/vChina与混凝土抗拉强度ft之间的关系图。图中可以看出,随着ft的增加,vtest/vChina<1的点越多,说明混凝土强度越高,中国规范计算的抗剪强度安全度越低。从图中还可以看出vtest/vChina<1的点多为剪跨比λ>3的梁,可见中国规范对于大剪跨比的高强混凝土梁不够安全。图8 为抗剪强度试验值与美国规范计算值比值vtest/vACI与混凝土抗压强度fc之间的关系图,图中几乎所有的点都在vtest/vACI=1以上,可见美国规范用于高强混凝土无腹筋梁抗剪强度计算是安全的。
4.2 剪跨比
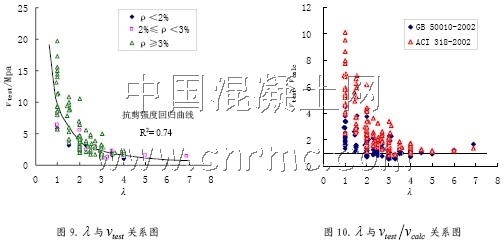
梁的剪跨比反映了梁的剪切破坏形态,是梁抗剪强度的主要影响因素。图9 给出了梁的剪跨比与抗剪强度试验值之间的关系,可以看出,剪跨比与抗剪强度的相关性较好。当剪跨比由小增大时,在λ<2 区间,抗剪强度下降很快;2≤λ≤3区间,抗剪强度的变化已经很小。λ>3以后,剪跨比对梁的抗剪强度影响不大。这主要是因为梁在抗剪过程中同时存在“梁作用”和“拱作用”λ<3时“拱作用”较大,而λ>3以后“拱作用”逐渐减弱造成的。图10 为剪跨比与抗剪强度试验值与计算值的比值test calc v v 的关系图,图中给出了试验值与中国规范计算值的比值点和试验值与美国规范计算值的比值点。可见在剪跨比λ < 2 时,两国规范数据点均在vtest/vcalc=1以上,说明两国规范公式在此区间都是安全的,但是美国规范比中国规范要保守;而当λ≥2 时,中国规范有相当一部分点落在了vtest/vcalc=1以下,说明中国规范公式对于大剪跨比的梁不安全;美国规范当λ>3时也不安全。
4.3 梁的尺寸效应
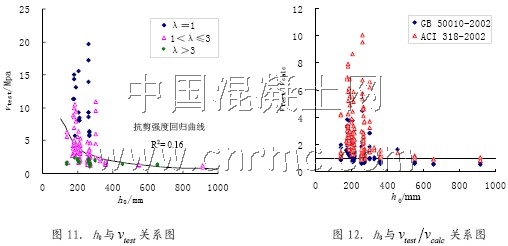
试验数据分析表明,无腹筋梁的抗剪强度受尺寸效应的影响。即在混凝土强度、纵筋配筋率和剪跨比一定的情况下,随着梁的有效截面高度增加,抗剪承载力呈下降趋势,如图11 所示。尺寸效应的原因可以解释为,随着截面高度的增加,在斜裂缝的宽度增大,骨料之间的咬合作用削弱,导致承载能力下降。图11 还表明尺寸效应的大小与剪跨比密切相关,对于λ>3的梁,有效高度对抗剪强度几乎没有影响。
图12 为试验值与计算值随梁截面高度变化的关系图,图中可以看出当梁截面有效高度大于200mm时,有不少中国规范计算值小于试验值,而我国规范规定的截面高度影响系数的起点是800mm,相对来说安全性不足。美国规范也有少数点落在了vtest/vcalc=1一下,说明其对尺寸效应的考虑也不充分。Kim[8]的试验也得到同样的结果,并且证明ACI 规范公式用于d=915mm 的高强混凝土无腹筋梁的抗剪强度计算是不安全。
4.4 纵筋配筋率
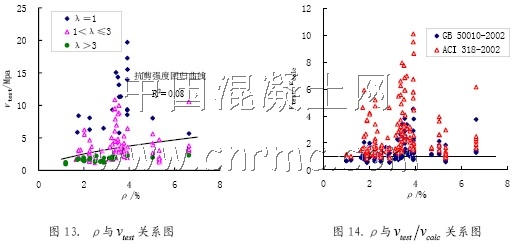
纵向钢筋除了直接提供销栓力以外,还使梁的中和轴降低,从而加大了斜裂缝顶部混凝土受压区高度,间接提高梁的抗剪承载力。图13 给出了纵筋与抗剪强度之间的关系,可见随着纵筋配筋率的增加,梁的抗剪强度增大,但是数据离散性很大,纵筋配筋率与梁的抗剪强度的相关性较差。图中还显示对于小剪跨比的梁,纵筋配筋率对抗剪强度影响较大,但是当剪跨比λ > 3时,增大纵筋率对梁的抗剪承载力几乎没有影响。图14 则表明了梁抗剪强度试验值与计算值的比值随纵筋配筋率之间的关系,图中无论是用中国规范还是用ACI 规范计算,均有部分数据点落在了vtest/vcalc=1以下,
可见两国规范都没有合理考虑这一影响因素,中国规范相对ACI 规范可靠性更低。
5 结论
本文收集国内外学者关于集中荷载作用下的高强混凝土无腹筋梁抗剪试验数据158个,将试验结果分别与中国规范GB50010-2002、美国规范ACI 318-2002提供的抗剪强度计算公式计算结果进行分析比较,得出以下结论:
(1)中国规范抗剪公式对于小剪跨比的梁偏于保守,对大剪跨比的梁不够安全,没有合理考虑尺寸效应和纵筋配筋率对梁抗剪承载力的影响,总体可靠度偏低。
(2)美国规范抗剪公式高估了混凝土抗压强度的影响,低估甚至忽视了剪跨比、尺寸效应和纵筋配筋率对梁抗剪承载力的影响,对于剪跨比大于3 的梁不安全,总体可靠度较高,并且偏于保守。
参考文献:
[1] 陈肇元,朱金拴,吴佩刚.高强混凝土及其应用[M].北京:清华大学出版社,1992.
[2] 施岚清. 混凝土强度(140#~1100#)对无腹筋梁抗剪强度影响的试验研究[R]. 清华大学土木系,海后设计局.1981,3
[3] Andew.G.Mphorde and Gregory. C. Frantz. Shear test of high-and low-strength concrete beams without stirrups[J]. ACI Journal, 1984,81(4):350-357
[4] Shuaib H. Ahmad,A.R.Khaloo,A. Poveda. Shear Capacity of Reinforced High-strength Concrete Beams[J]. ACI Journal,1986,83(2):197-305
[5] Ashraf H. Elzanaty,Arthur H. Nilson,Floydo. Slate. Shear Capacity of
Reinforced Concrete Beams Using High Strength Concrete[J]. ACI Journal, 1986,83(2):296-298
[6] Mark K. Johnson and Julio A. Ramirez. Minimum Shear Reinforcement in
Beams With Higher Strength Concrete[J]. ACI Structural Journal, 1988,86(4):376-382
[7] 赵光仪,吴佩刚,赵成文等.高强混凝土受弯构件的抗剪强度[J].土木工程学报,1991,24(2):10-18
[8] Jin-Keun Kim, Yon-Dong Park. Shear strength of reinforced high strength
concrete beams without web reinforcement[J]. Magazine of Concrete Research,
1994,46(166):7-16
[9] YoungSoo Yoon,William D.Cook, Denis Mitchell. Minimum Shear
Reinforcement in Normal, Medium, and High-Strength Concrete Beams[J]. ACI
Structural Journal, 1996,93(5):576-584
[10] Sung-Woo Shin, Kwang-Soo Lee, JungIll Moon, S.K.Ghosh. Shear Strength
of Reinforced High-Strength Concrete Beams with Shear Span-to-Depth Ratios between 1.5 and 2.5[J]. ACI Structural Journal, 1999,96(4):549-556
[11] Raghu S. Pendyala, Priyan Mendis. Experimental Study on Shear
Strength of High-Strength Concrete Beams[J].ACI Structural Journal, 2000,97(4):564-571
[12] F. J. Vecchio, W. Shim. Experimentral and Analytical Reexamination
of Classic Concrete Beam Tests[J]. Journal of Structural Engineering, ASCE,
2004,130(3):460-469
[13] 支运芳等.集中荷载作用下超高强混凝土无腹筋梁抗剪强度的试验研究[J].重庆工学院学报,2005,19(3):69-75
[14] A. Cladera, A. R. Mari. Experimental Study on High Strength Concrete
Beams Failing in Shear[J]. Engineering Structures, 2005,27:1519-1 527
[15] Ahmed K, El-Sayed, Ehab F.ElSalakawy, Brahim Benmokane. Shear
Capacity of High-Strength Concrete Beams Reinforcement with FPP
Bars[J]. ACI Structural Journal, 2006,103(3):383-389

















